通过固定概率事件获取任意概率事件

获取任意概率函数

举个例子，有一枚硬币，抛出后正面朝上的概率为$q$，这个问题等价于如何通过多次抛一枚硬币获取概率为$p$的事件。

事实上，可以多次组合抛硬币事件来实现。下面我们的任务是组合多个事件让它们的概率之和等于$p$。设最终求出的事件为S，在此做个规定，S包括或包括于第一次正面向上衍生的事件。

第一次抛，正面向上的概率是$q$，反面朝上的概率是$1-q$。

• 如果$p\leq q$，则S应该包括于第一次正面向上衍生的事件。

  如果抛出正面朝上，接下来在第一次正面向上衍生的事件中寻找概率和为$p$的事件即可，相当于从第一次开始抛硬币，找出概率为$\frac{p}{q}$的事件，这是因为

  $$\begin{aligned} P(S|第一次正面向上衍生的事件)&=\frac{P(S\cap{第一次正面向上衍生的事件})}{P(第一次正面向上衍生的事件)} \\&=\frac{P(S)}{P(第一次正面向上衍生的事件)}\\&=\frac{p}{q} \end{aligned}$$

  所以$S\cap{第一次正面向上衍生的事件}=S$。

  在反面朝上发生的情况下，由于S是包括于第一次正面向上衍生的事件的，所以反面朝上衍生的事件不可能和S有交集，因此返回False。

• 如果$p>q$，则S应该包括第一次正面向上衍生的事件。

  如果正面朝上直接返回True即可；

  在反面的情况下，需要在第一次反面朝上衍生的事件中寻找概率和为$p-q$的事件，相当于从零开始抛硬币，找出概率为$\frac{p-q}{1-q}$的事件族。

  $$\begin{aligned} P(S|第一次反面向上衍生的事件)&=\frac{P(S\cap{第一次反面向上衍生的事件})}{P(第一次反面向上衍生的事件)}\\&=\frac{P(S-第一反面向上衍生的事件)}{P(第一次反面向上衍生的事件)}\\&=\frac{p-q}{1-q}。 \end{aligned}$$

接下来递归即可。
上面的解释比较抽象，可以用数形结合的方式：

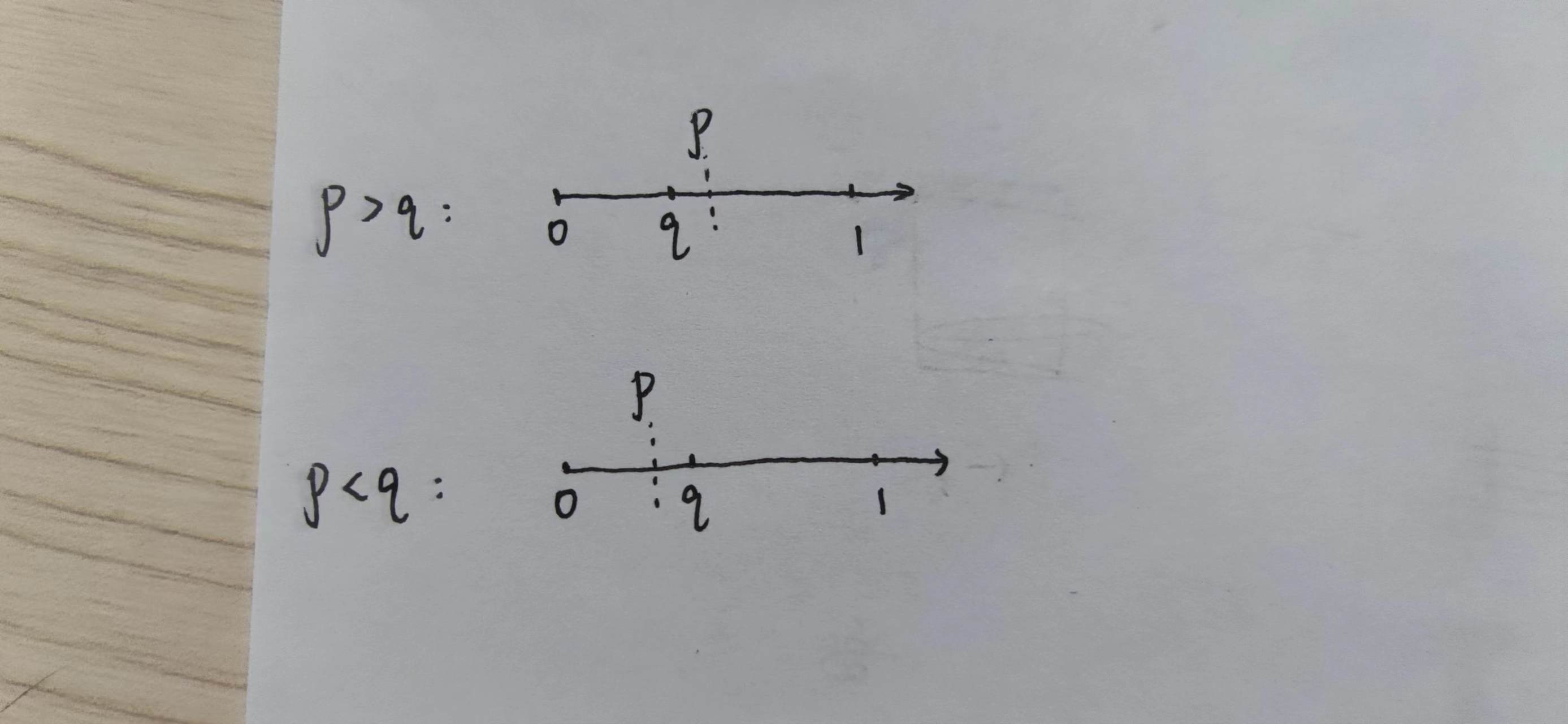
我们的目的是要求一个数确定性地落在$[0,p]$区间，现在只知道这个数是不是落在$[0,q]$区间。

• 情况1：$p>q$。如果第一次就落在了$[0,q]$区间，肯定满足落在$[0,p]$区间的要求，直接返回true；如果落在$[q,1]$区间，需要确保它落在[q,p]区间，此时将[q,1]放缩到[0,1]，[q,p]放缩为$[0,\frac{p-q}{1-q}]$，相当于重新抛硬币获取概率为$\frac{p-q}{1-q}$的事件。
• 情况2：$p<q$。如果第一次就落在了$[q,1]$区间，肯定不满足落在$[0,p]$区间的要求，直接返回false；如果落在$[0,q]$区间，需要确保它落在[0,p]区间，此时将[0,q]放缩到[0,1]，[0,p]放缩为$[0,\frac{p}{q}]$，相当于重新抛硬币获取概率为$\frac{p}{q}$的事件。

测试代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

import random

q = 0.1

def toss_coin(p):
    """
    抛硬币，返回正面的概率为 p
    :param p:
    :return:
    """
    return lambda: random.random() < p


def get_prob(p, my_rand):
    if p <= q:
        if my_rand():
            return get_prob(p / q, my_rand)
        else:
            return False
    else:
        if my_rand():
            return True
        else:
            return get_prob((p - q) / (1 - q), my_rand)


def test(p):
    sum = 0
    N = int(1e7)
    for i in range(N):
        if get_prob(p, toss_coin(q)):
            sum += 1
    return sum / N


print(test(0.5))

拓展：

470. 用 Rand7() 实现 Rand10() - 力扣（LeetCode）

思路：这道题可以用Rand7()生成等概率的49个数，然后划分出相等的10个区间，用拒绝采样策略舍弃掉剩余的区间。不过这种题其实有通解，如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

# The rand7() API is already defined for you.
# def rand7():
# @return a random integer in the range 1 to 7

class Solution:
    def rand10(self):
        """
        :rtype: int
        """
        def rand():
            if rand7() < 4:
                return True
        def rand2():
            idx1 = 1 if rand() else 0
            idx2 = 1 if rand() else 0
            if idx1 == 0 and idx2 == 1:
                return 0
            elif idx1 == 1 and idx2 == 0:
                return 1
            else:
                return rand2()
        while True:
            ans = 0
            for _ in range(4):
                ans <<= 1
                ans |= rand2()
            if ans < 10:
                return ans + 1