KMP 算法 - 算法学习 | Foufor Past = FP 的一亩三分地

KMP算法简要介绍

KMP算法可以高效地在一个文本串T（长度为n）中查找模式串P（长度为m）的出现位置。

首先看一下蛮力匹配的匹配过程。

屏幕截图 2021-12-31 143350

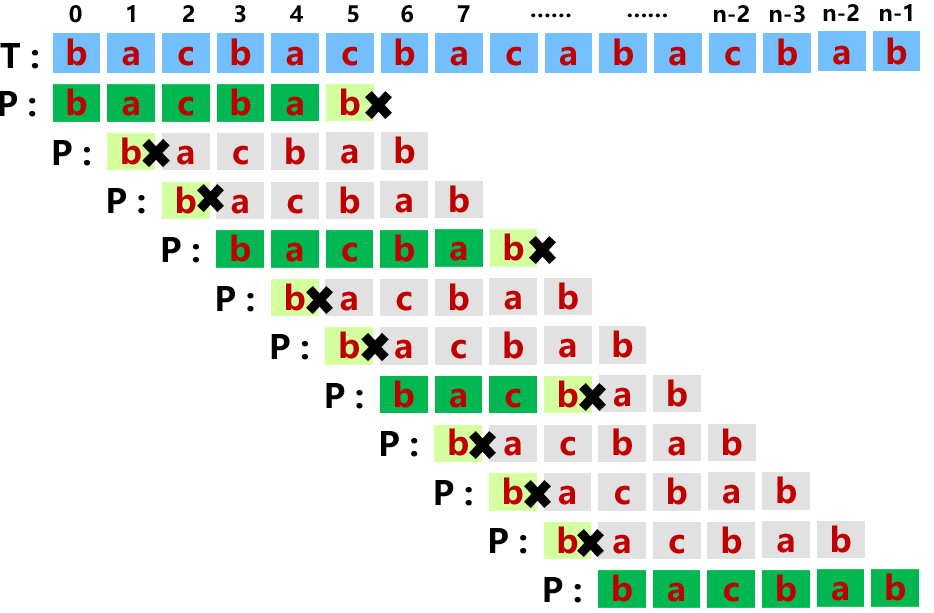
蛮力匹配中，如果P在位置j和T在位置i失配，P会回退到位置0，T的位置＋1，然后二者重新开始比对。这种算法的平均复杂度是O(m*n)。

可以看到，实际上P[5]和T[5]失配后，实际上可以直接从P[2]和T[5]开始比对，这是因为第一次比对的过程中，我们得到了P[0:4]==T[0:4]的信息，因此第二次比对实际上是P[0:3]和P[1:4]之间的比对，第三次比对是P[0:2]和P[2:4]之间的比对，如果我们可以预处理P字符串，得到P[0:3]!=P[1:4]，P[0:2]!=P[2:4]，P[0:1]==P[3:4]的信息，我们就可以跳过第二次和第三次比对，直接从P[2]和T[5]比对开始。如此以来我们不需要回退T的指针，可以将复杂度压缩到O(n)。

那么我们怎么从P[5]和T[5]失配得到下一次应该比对的是P[2]和T[5]呢，实际上，我们只需要找到P[0:4]的最大长度的相匹配的真前缀和真后缀即可。即如果P在位置j失配，下次比对的位置应该为

$next[j]=max(\{0\leq t<j|P[0,t)==P[j-t,j)\})$

以bacbab为例

j=0，next[0] = -1（假想P[-1]为通配）
j=1, b没有真前缀和真后缀，因此next[1]=0
j=2, ba的真前缀为{b}，真后缀为{a}，没有共有元素，因此next[2]=0
j=3，bac的真前缀为{b,ba}，真后缀为{ac,c}，没有共有元素，因此next[3]=0
j=4, bacb的真前缀为{b,ba,bac}，真后缀为{acb,cb,b}，二者最大长度的共有元素为b，长度为1，因此next[4]=1
j=5，bacba的真前缀为{b,ba,bac,bacb}，真后缀为{acba,cba,ba,a}，二者最大长度的共有元素为ba,因此next[5]=2

下面用代码计算next表

// next[i]代表了如果模式串P在i处和主串T的第j个位置失配，下一次应该比较模式串的第next[i]个位置和主串的第j个位置
// next[i] = max{k | k < i && p[0...k-1] == p[i-k...i-1]}
vector<int> buildNext(string& P) {
    int m = P.size();
    int j = -1;  // j代表了模式串的下标（这里的模式串就是P[0:j]）
    vector<int> next(m, -1);
    for (int i = 1; i < m; ++i) { // i代表主串的比对下标（这里的主串就是P[0:i]
        if (j < 0||P[i - 1] == P[j]) {   // 如果匹配成功
            ++j;
            next[i] = j;
        }
        else {   // 如果匹配失败,按照next[i]的定义,j回溯到上一个匹配的位置
            while (j >= 0 && P[i - 1] != P[j]) {
                j = next[j];
            }
            // 跳出上面的循环要么是j = -1,要么是P[i - 1] == P[j]，这两种情况都需要对j+1,
            // 如果在P[i]处和T[idx]失配，说明P[:i]==T[idx-i:idx]，由next的定义，P[:next[i]] == P[i-next[i]:i] == T[idx-next[i]:idx]，
            // 下一次需要比较P[next[i]]和T[idx]，所以j要加1
            ++j;
            next[i] = j; 
        }
    }
    return next;
}


int strStr(string T, string P) {
    vector<int> next = buildNext(P);
    int j = 0;
    for (int i = 0; i < T.size(); ++i) {
        if (T[i] == P[j]) {   // 如果匹配成功
            ++j;
            if (j == next.size()) {
                return i - j + 1;
            }
        }
        else {   // 如果匹配失败,按照next[i]的定义,j回溯到上一个匹配的位置
            while (j >= 0 && T[i] != P[j]) {
                j = next[j];
            }
            // 跳出上面的循环要么是j = -1,要么是P[i] == P[j]，这两种情况都需要对j+1
            ++j;
        }
    }
    return -1;
}

精简版本：

vector<int> buildNext(string& P) {
    int m = P.size();
    int j = -1;  // j代表了模式串的下标（这里的模式串就是P[0:j]）
    vector<int> next(m, -1);
    for (int i = 1; i < m; ++i) { // i代表主串的比对下标（这里的主串就是P[0:i]
        while (j >= 0 && P[i - 1] != P[j]) {
            j = next[j];
        }
        ++j;
        next[i] = j;
    }
    return next;
}


int strStr(string T, string P) {
    vector<int> next = buildNext(P);
    int j = 0;
    for (int i = 0; i < T.size(); ++i) {
        // 如果匹配失败,按照next[i]的定义,j回溯到上一个匹配的位置
        while (j >= 0 && T[i] != P[j]) {
            j = next[j];
        }
        // 跳出上面的循环要么是j = -1,要么是P[i] == P[j]，这两种情况都需要对j+1
        ++j;
        if (j == next.size()) {
            return i - j + 1;
        }
    }
    return -1;
}

另外一种版本：

vector<int> buildNext (string& P) {
    int m = P.size();
    int j = 0;
    int t = -1;
    vector<int> next(m, -1);
    while(j < m - 1){
        if(t == -1 || P[j] == P[t]){ // 一直匹配的情况
            ++j;
            ++t;
            next[j] = t;
        }
        else{   // 失配的情况
            t = next[t];
        }
    }
    return next;
}
int find(string P, string T){
    int m = P.size(), n = T.size();
    vector<int> next = buildNext(P);
    int i = 0, j = 0;
    while(i < n){
        if(j == -1||T[i] == P[j]){
            ++i;
            ++j;
            if(j == m){
                return i - m;
            }
        }
        else{
            j = next[j];
        }
    }
    return -1;
}

时间复杂度：设 $k=2i-j$ ，每次while循环如果满足$j == -1||T[i] == P[j]$则k严格增加1，如果不满足由于$j=next[j]$，即j至少会增加1，则k至少会减小1。所以while循环不会超过k次。由于$k\leq2i{max}-j{min}$，所以$k\leq2n+1$，所以时间复杂度为O(2*n+1)，即O(n)

其实上面的next表计算的是字符串P的真前缀的所有真前缀和真后缀中相同子串的最大长度，并没有计算P自身的所有真前缀和真后缀中相同子串的最大长度，如果是想计算后者，一种方法是在P后追加一个字符，计算这个新的字符串的next表，取next[1:end]即可；另一种方法是修改计算next的逻辑，代码如下：

（这里面计算出来的值相当于是$len[j]=max({0\leq t<j|P[0,t)==P(j-t,j]})$，在原始的next数组基础上整体向前移动一个元素，等价于下面的java代码）。

vector<int> getMaxPreSuf (string& P) {
    int m = P.size();
    int j = 1;
    int t = 0;
    vector<int> len(m, 0);
    while(j <= m - 1){
        if(P[j] == P[t]){
            t++;
            len[j] = t;
            j++;
        }
        else if (t != 0){
            t = len[t - 1];
        } else{
            j++;
        }
    }
    return len;
}

~~再引申一下，如何计算字符串P的所有前缀和字符串Q的所有后缀中相同子串的最长长度，实际上修改一下上面的getMaxPreSuf函数就行了。~~

/*
int getMax (string P, string Q) {
    int m = P.size(), n = Q.size();
    int start = m > n? 0:n - m;
    int j = start + 1;
    int t = 0;
    vector<int> len(min(m, n), 0);
    while(j < n){
        if(Q[j] == P[t]){
            t++;
            len[j - start] = t;
            j++;
        }
        else if (t != 0){
            t = len[t - 1];
        } else{
            j++;
        }
    }
    return len.back();
}
*/

ps：计算前缀表的另外一种方法，这种方法的next数组含义是P[j]和T[i]失配后，应该比较P[next[j-1]]和T[i]，这里的next[i]表示P[:i+1]的最大公共前后缀。

class Solution {
    public int strStr(String haystack, String needle) {
        int[] next = getNext(needle);
        int j = 0;
        for(int i = 0; i < haystack.length(); ++i){
            if(haystack.charAt(i) == needle.charAt(j)){
                j++;
                if(j == next.length){
                    return i - j + 1;
                }
            }else{
                while(j > 0&&haystack.charAt(i) != needle.charAt(j)){
                    j = next[j - 1];
                }
                if(haystack.charAt(i) == needle.charAt(j)){
                    j++;
                }
            }
        }
        return -1;
    }

    public int[] getNext(String needle){
        int[] next = new int[needle.length()];
        next[0] = 0;
        int j = 0;
        for(int i = 1; i < needle.length(); ++i){
            if(needle.charAt(i) == needle.charAt(j)){
                j++; // next[i]表示P[:i+1]的最大公共前后缀,例如aabaa，i=4,j=1(=> j=2)
                next[i] = j;
            }else{
                // 失配的情况下回到上一个匹配的位置
                while(j > 0&&needle.charAt(i) != needle.charAt(j)){
                    j = next[j - 1];
                }
                // 上一个位置如果匹配，j++
                if(needle.charAt(i) == needle.charAt(j)){
                    j++;
                }
                next[i] = j;
            }
        }
        return next;
    }
}

上面的代码仍然可以精简

public int strStr(String haystack, String needle) {
    int[] next = getNext(needle);
    int j = 0;
    for(int i = 0; i < haystack.length(); ++i){
        while(j > 0&&haystack.charAt(i) != needle.charAt(j)){
            j = next[j - 1];
        }
        if(haystack.charAt(i) == needle.charAt(j)){
            j++;
        }
        if(j == next.length){
            return i - j + 1;
        }
    }
    return -1;
}

public int[] getNext(String needle){
    int[] next = new int[needle.length()];
    next[0] = 0;
    int j = 0;
    for(int i = 1; i < needle.length(); ++i){
        // 失配的情况下回到上一个匹配的位置
        while(j > 0&&needle.charAt(i) != needle.charAt(j)){
            j = next[j - 1];
        }
        // 上一个位置如果匹配，j++
        if(needle.charAt(i) == needle.charAt(j)){
            j++;
        }
        next[i] = j;
    }
    return next;
}

算法字符串

遥感多模态综述